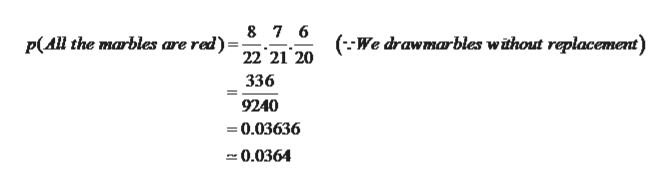A Bag Contains 8 Red Marbles 6 Blue Marbles

Given that you have bb.

A bag contains 8 red marbles 6 blue marbles. There s one blue marble. The first marble is returned in the bag before drawing the second. A draw the tree diagram for the experiment. B the probability that both are the same color.

C the probability that the second marble is blue. You have 8 6 4 18 marbles each assumed to have a 1 18 probability of being drawn. There are 8 6 48 ways of drawing blue then red so p 8 6 18 18 4 3 9 9 4 3 9 4 27 0 148148148 or just under 15. We will assume that only two marbles are drawn from the bag and hence there are two cases.

What is the probability of selecting a red marble replacing it in the bag and then selecting a green marble. There s two red marbles in the bag. The probability that all the marbles are red is b. If three marbles are drawn out of the bag what is the probability to the nearest 1000th that all three marbles drawn will be blue.

So i could pick that green marble or that green marble. So this is all the possible outcomes. Randomly choose two marbles one at a time and without replacement. A jar contains 4 black marbles and 3 red marbles.

Two marbles are drawn without replacement from a jar containing 4 black and 6 white marbles. A bag contains 8 red marbles 7 white marbles and 7 blue marbles. B find probabilities for p bb p br p rb p ww p at least one red p exactly one red 3. Two marbles are drawn without replacement.

These are clearly all yellow. A bag contains 8 blue marbles 6 red marbles and 4 green marbles. A the probability that the first marble is red and the second is white. There s two green marbles in the bag.

You draw 3 marbles out at random without replacement. The probability that none of the marbles are red is. A bag contains 8 red marbles 6 blue marbles and 3 green marbles. Find p red and blue.

A bag contains 8 red marbles 4 white marbles and 5 blue marbles. The first marble is not returned in the bag before drawing the second. Find the following probabilities and round to 4 decimal places a.